Methodological Information
Knowledge Synthesis: A Working Framework
Our methodological approach has its roots in an operational bayesian framework of Knowledge Synthesis. The Knowledge Synthesis framework relies on some plain characteristics, as shown in the following table.
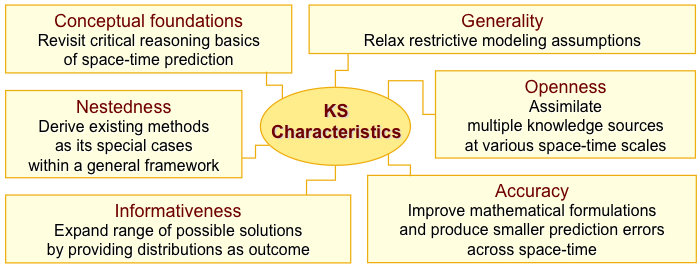
Knowledge Synthesis reviews the conceptual foundation for spatiotemporal prediction, in that it uses physical principles that make sense in the context of analysis within the space-time continuum. For example, it is important to define correctly the spatiotemporal distance in a three-dimensional continuum of two spatial dimensions and time according to the study conditions and applicable geometry; in this manner, one must define spatiotemporal distances in an appropriate way when studying a problem on a plane, on a sphere, in city blocks, etc.
In extension to the revision characteristic, it is acknowledged that classical predictive methodologies in statistics are bound by traditional restrictive assumptions. The proposed framework enables methodologies that operate free from such assumptions and make better physical sense. For example, the common assumption of Gaussianity in the distributions of observed data is necessary for linear model and likelihood based prediction techniques. Although this can be an occasionally valid assumption, it can introduce significant bias in a study when nature behaves in a different manner.
Knowledge Synthesis techniques are conceived as extensions of classical existing methodologies, rather than replacement or completely foreign entities. Classical prediction techniques have been derived as special cases of the former, which naturally puts Knowledge Synthesis techniques in the category of scientific theories that are themselves subject to testing, revision and expansion.
Techniques in the Knowledge Synthesis framework feature some very attractive characteristics for spatiotemporal analysis. Namely, to improve prediction accuracy, the framework embraces informative sources of a variety of types beyond attribute observations. These sources can be knowledge bases such as natural models, physical laws, differential equations, and even observations that carry uncertainty in the form of interval data or distributions. Accounting for known uncertainty in the input might possibly produce increased prediction error, but leads in more informed output than a potentially erroneous assumption of exact input values. Finally, the framework enables prediction in the form of complete probability density functions, even in cases when the input is non-Gaussian. Knowledge of full probability density functions offers you a broad selection of ways to express your output in the most appropriate manner for your analysis; for example, you can select the distribution mode to report the most probable value in your prediction.
Analysis Techniques
A couple of more popular and better-developed techniques under the Knowledge Synthesis framework are the so called Bayesian Maximum Entropy, or BME, and the Generalized BME, or GBME.
The BME theory considers a prior stage where general knowledge bases are integrated in the analysis. General knowledge bases are typically process-related principles, models and laws that govern the process. These are accounted for in advance to produce the prior probability density function of the analysis. The analysis concludes with the integration of case specific information into the prior to produce the posterior (or prediction) probability density function. This analytical procedure is based on an operational use of the Bayes law for prediction that is conditional to prior information. To yield the most accurate prediction, one tries to maximize the initial information, which is equivalent to the negative entropy in physical sciences; hence, the derivation of the technique name.
The GBME theory is mainly a slight variation of the BME analytical procedure in the prior stage. Specifically, GBME performs prediction in the same manner as BME does. Yet, before the predictive segment of the analysis, GBME explores heterogeneities and spatiotemporal correlation at a local level. Whereas BME requires an earlier analysis of field heterogeneities to remove mean (surface) trends from the whole field of interest, GBME performs this analysis by means of space-time increments at local neighborhoods. Similarly for correlations, whereas BME assumes a correlation dependence for the entire domain of interest, GBME selects from a set of generalized covariance functions the most applicable one at a local scale.
The difference in the BME and GBME approaches enables you the flexibility to select a Knowledge Synthesis technique that best describes your process on the basis of the process physical characteristics. Both approaches advance by integrating your case-specific observations into their prior distributions, and they subsequently deliver the prediction in the form of the posterior probability density function.